分火腿
1s,64MB
题目描述
小月言要过四岁生日了,她的妈妈为她准备了n根火腿,她想将这些火腿均分给m位小朋友,所以她可能需要切火腿。为了省事,小月言想切最少的刀数,使这n根火腿分成均等的m份。请问最少要切几刀?
输入
第一行一个整数T,表示有T组数据。
接下来T组数据,每组共一行,有两个数字n,m。
输出
每组数据一行,输出最少要切的刀数。
样例输入
样例输出
提示&约定
100%的数据保证T<=1000;n,m<=2147483647。
solution
考虑把所有的火腿连成一根,那么一定会切m-1刀
什么情况下可以少切呢?在某些需要切刀的地方,火腿由两根火腿拼接,比如分成6段,有2根火腿,则切成3-3中间这刀不用切。
经过观察发现少切的刀数是$gcd(n,m)$
所以答案为$m-gcd(n,m)$
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| #include<bits/stdc++.h>
#define ll long long
#define fsb(a,b,c) for(register int a=b;a<=(c);a++)
#define fbs(a,b,c) for(register int a=b;a>=(c);a--)
using namespace std;
int n,a,b,T;
template<typename qw>inline void rll(qw &x){
qw f=1;x=0;char c=getchar();
while(!isdigit(c))f=c=='-'?-1:f,c=getchar();
while(isdigit(c))x=x*10+c-'0',c=getchar();
x*=f;
}
inline ll gcd(ll a,ll b){
return b==0?a:gcd(b,a%b);
}
int main(){
freopen("hdogs.in","r",stdin);freopen("hdogs.out","w",stdout);
rll(T);
fsb(i,1,T){
rll(a);rll(b);
printf("%lld\n",b-gcd(a,b));
}
return 0;
}
|
无聊的会议
1s,128MB
题目描述
土豪学长作为一名光荣的学生会干部,每天要参加很多无聊的会议。他发现:他开会的会议桌一定是正n边形,n个干部坐在这个多边形顶点上。因为太无聊了,所以他想要数出所有的“完全”等腰三角形——这种等腰三角形的三个顶点一定全是给出n多边形的顶点,且三个顶点上坐的干部性别相同。
土豪学长是土豪,他用1000000000%10的佣金雇用你,让你帮他数。PS:如果两个“完全”等腰三角形三个顶点相同,计算时只算一个。
输入
第一行一个数字T,表示有T组数据。
接下来有T组数据,每组数据共一行。这一行给出一个长度为n的字符串,表示正n边形n个顶点上干部的性别。1为男,0为女。
输出
对于第i组数据:输出”Case i: ans”(不带引号),ans为“完全”等腰三角形的数量。
样例输入
1
2
3
4
5
6
| 5
0001
01
10001
1101010
111010
|
样例输出
1
2
3
4
5
| Case 1: 1
Case 2: 0
Case 3: 1
Case 4: 3
Case 5: 2
|
提示&约定
40%的数据保证n<=20
100%的数据保证 n<=10^6
所有数据保证T<=10
solution
这个题有点有趣。
考试的时候我只会$n^2$
考虑怎么搞正解。
首先我们可以搞出所有等腰三角形,然后减去这些三角形中颜色不一样的
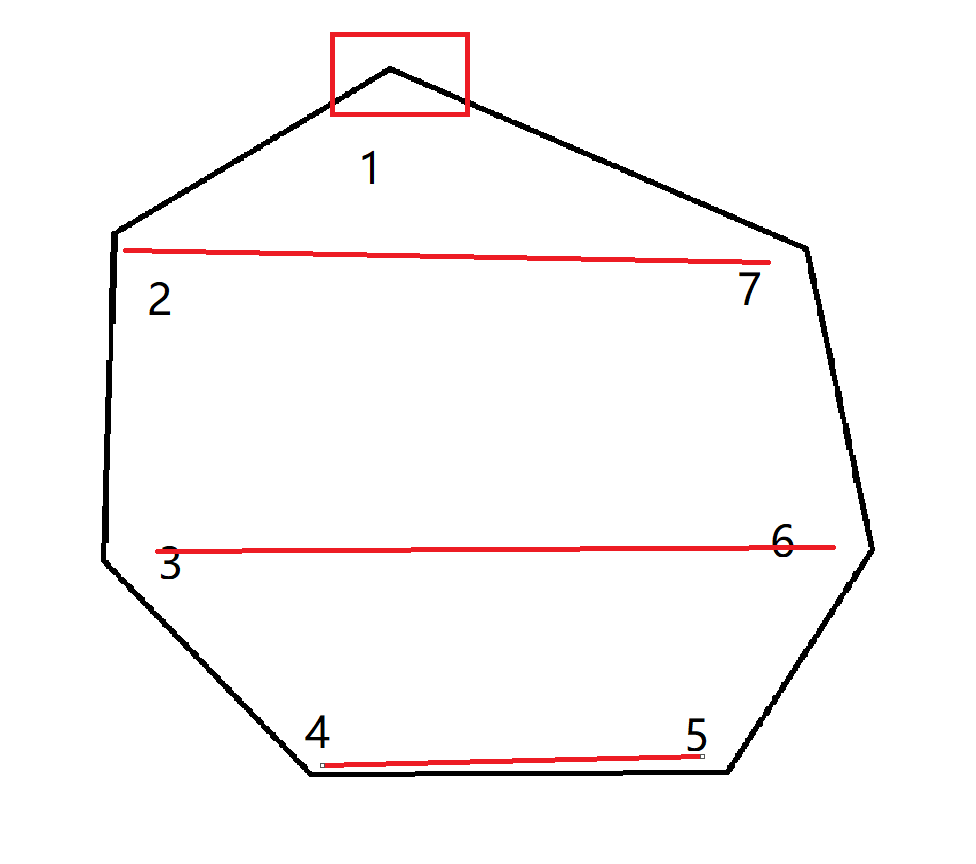
选中一个点,剩下的点关于它两两对称,可以组成$(n-1)/2$(下取整)对。因此共有$n·((n-1)/2)$个等腰三角形。
考虑去掉等边三角形重复,所以共有$n·((n-1)/2)-(n\%3==0?n/3*2:0)$个等腰三角形。
接下来去掉颜色不同的等腰三角形
要分点数为奇偶两种情况讨论(因为如果选中两个点为底,他们能构成的等腰三角形个数与点的奇偶有关)。
奇数

对于一对颜色不同的点,他们被多计算了3次(能构成3个等腰三角形),因此统计白点数s0,黑点数s1,总共多计算$s0 · s1 · 3$次。
但是对于一个等边三角形应该只多计算了一次,因此如果$n\%3==0$,总共多计算$s0 · s1 · 3 - n/3·2$次。
偶数
有两种情况,一种是这样的

一对颜色不同的点被多算了2次。
另一种是

一对不同颜色的点被多算了4次。
我们发现这和编号奇偶性有关,分别记
|
编号偶 |
编号奇 |
| 颜色0 |
s00 |
s10 |
| 颜色1 |
s01 |
s11 |
总共多算了$2(s00·s11+s10·s01)+4(s01·s00+s10·s11)$(记为ans)次。
考虑n是3的倍数,若n是3的倍数,总共多算了$ans-n/3·2$次
n为偶数时还有一种不成立的情况,即底边为0。
因此对于每一对相对(如0号点和(n+1)/2号点)的点,如果颜色不一样,则ans—
最后,无论n是奇数还是偶数
点A和点B会算一次重复,点B和点A会再算一次,因此ans/=2
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
| #include<bits/stdc++.h>
#define ll long long
#define N 1000010
#define md(a) ((a)<n?(a):((a)-n))
#define fsb(a,b,c) for(register int a=b;a<=(c);a++)
#define fbs(a,b,c) for(register int a=b;a>=(c);a--)
using namespace std;
ll n,T;
char a[N];
template<typename qw>inline void rll(qw &x){
x=0;qw f=1;char c=getchar();
while(!isdigit(c))f=c=='-'?-1:f,c=getchar();
while(isdigit(c))x=x*10+c-'0',c=getchar();
x*=f;
}
inline ll calc(){
return n*((n-1)/2)-(n%3==0?n/3*2:0);
}
inline ll mi(){
ll ans=0;
if(n&1){
ll s0=0,s1=0;
fsb(i,0,n-1)if(a[i]=='0')s0++;else s1++;
ans=s0*s1*3;
if(n%3==0){
ll s0=n/3,s1=s0*2;
fsb(i,0,n-1){
ans-=(a[i]!=a[md(i+s0)])?1:0;
ans-=(a[i]!=a[md(i+s1)])?1:0;
}
}
}else{
ll s00=0,s01=0,s10=0,s11=0;
for(int i=0;i<n;i+=2)if(a[i]=='0')s00++;else s01++;
for(int i=1;i<n;i+=2)if(a[i]=='0')s10++;else s11++;
ans=s00*s11*2+s10*s01*2+s10*s11*4+s01*s00*4;
ll t=n/2;
fsb(i,0,n-1)ans-=a[i]!=a[md(i+t)]?1:0;
if(n%3==0){
s00=n/3;s01=s00*2;
fsb(i,0,n-1){
ans-=(a[i]!=a[md(i+s00)])?1:0;
ans-=(a[i]!=a[md(i+s01)])?1:0;
}
}
}
return ans/2;
}
int main(){
freopen("meeting.in","r",stdin);freopen("meeting.out","w",stdout);
rll(T);
fsb(TT,1,T){
scanf("%s",a);n=strlen(a);
printf("Case %d: %lld\n",TT,calc()-mi());
}
return 0;
}
|
班服
1s,128MB
问题描述
要开运动会了,神犇学校的n个班级要选班服,班服共有100种样式,编号1~100。现在每个班都挑出了一些样式待选,每个班最多有100个待选的样式。要求每个班最终选定一种样式作为班服,且该班的样式不能与其他班级的相同,求所有可能方案的总数,由于方案总数可能很大,所以要求输出mod 1000000007后的答案。
输入
共有T组数据。
对于每组数据,第一行为一个整数n,表示有n个班级。
2~n+1行,每行有最多100个数字,表示第i-1班待选班服的编号。
输出
对于每组数据,输出方案总数 mod 1000000007后的答案。
样例输入
1
2
3
4
5
6
7
8
| 2
3
5 100 1
2
5 100
2
3 5
8 100
|
样例输出
提示&约定
对于30%的数据,1<=T<=3, 1<=n<=3,每班待选样式不超过10种。
对于50%的数据,1<=T<=5, 1<=n<=5,每班待选样式不超过50种。
对于100%的数据,1<=T<=10, 1<=n<=10,每班待选样式不超过100种。
solution
考虑到拿衣服匹配班级和拿班级匹配衣服是一样的,一个是10一个是100,于是对10搞状压DP
$f[i][j]$表示前i种衣服,班级穿衣状态为j的方案数
答案:$f[100][mx],mx=(1<<n)-1$,即所有衣服下,每个班级都有衣服的方案数。
初始化:显然$f[i][0]=1$,即不管你给多少衣服,没有一个班级穿衣服的方案数为1.
转移:考虑新加进一件衣服i,枚举班级j(班级j必须能穿i),枚举状态k(班级j在状态k中必须不穿衣服)
给班级j穿i。即$f[i][k+1<<j]+=f[i-1][k]$
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
| #include<bits/stdc++.h>
#define ll long long
#define mo 1000000007
#define md(a) ((a)%mo)
#define fsb(a,b,c) for(int a=b;a<=c;a++)
#define fbs(a,b,c) for(int a=b;a>=c;a--)
using namespace std;
int T,n,a[20][110],x,flag=0,mx;
ll f[110][1100];
template<typename qw>inline void rll(qw &x){
x=0;qw f=1;char c=getchar();
while(!isdigit(c)){
f=c=='-'?-1:f;c=getchar();
}
while(isdigit(c))x=x*10+c-'0',c=getchar();
x*=f;
if(c=='\n'||c=='\r'){
flag=1;return;
}
}
int main(){
freopen("shirt.in","r",stdin);freopen("shirt.out","w",stdout);
rll(T);
while(T--){
rll(n);mx=(1<<n)-1;memset(a,0,sizeof(a));
fsb(i,0,n-1){
flag=0;
while(1){
rll(x);a[i][x]=1;
if(flag)break;
}
}
memset(f,0,sizeof(f));
fsb(i,0,100)f[i][0]=1;
fsb(i,1,100){
fsb(j,0,mx)f[i][j]=f[i-1][j];
fsb(j,0,n-1){
if(!a[j][i])continue;
fsb(k,0,mx){
if(k&(1<<j))continue;
f[i][k+(1<<j)]=md(f[i][k+(1<<j)]+f[i-1][k]);
}
}
}
printf("%lld\n",f[100][mx]);
}
return 0;
}
|



